강화학습의 혈관 속 탐험 시리즈
강화학습의 혈관 속 탐험 (1) - 로봇과 심혈관 중재 시술
강화학습의 혈관 속 탐험 (2) - 강화학습과 제어 이론의 비교
강화학습의 혈관 속 탐험 (3) - 실험환경 구성과 강화학습 알고리즘 소개
Intro
이번 포스트에서는 저희가 왜 PCI 로봇 제어 방법으로 강화학습을 선택하게 되었는지 얘기해보고자 합니다. 이미 수많은 학자와 엔지니어들이 로봇을 위한 효율적이고 뛰어난 제어 이론들을 개발해왔습니다. 이러한 제어 이론들이 어떠한 점에서 강화학습과 다른지 살펴보겠습니다. 먼저, 제어 이론 중 가장 보편적이고 널리 쓰이는 PID 제어와의 비교로 시작하겠습니다.
PID Control
PID Control?
PID 제어는 Proportional-Integral-Derivative Control의 약자입니다. 현재 산업 현장의 80~90% 이상의 제어기는 이 PID제어 이론을 이용하여 동작을 수행합니다. 그 만큼 이 PID 제어에는 장점이 많습니다. 먼저 알고리즘이 코드 10줄 안에 끝날 정도로 가볍고, 사용하기 쉬우며, 제어 성능이 뛰어납니다. 하지만 이 PID 제어는 단순한 만큼 한가지 문제에만 집중합니다. 바로 Tracking 문제입니다.
아래 식은 PID 제어를 표현하는 가장 기본적인 식입니다. 아래 식을 살펴보면, 시간 $t$에서의 최종 출력 ${u}_t$는 목표 상태 ${x}_g$와 현재 상태 ${x}_t$의 차이, ${e}_t$에 의해서 결정되는 것을 알 수 있습니다. 즉, PID 제어는 목표 상태와 현재 상태를 가장 최단거리로 잇는 경로 위에서만 동작합니다 [1]. $${u}_t = {K}_p {e}_t + {K}_i \int_0^t {e}_t dt + {K}_d d{e}_t/dt$$
그림과 함께 좀 더 자세히 이야기해보겠습니다. 아래 그림에 목표 위치 ${x}_g$와 현재 위치 ${x}_t$가 있습니다. PID제어를 이용하면, ${l}_1$과 같은 경로로 현재 상태가 이동하게 됩니다. 제어기 설계에 따라서 속도가 느려지거나 빨라질 수도, 목표 지점을 넘어갈 수도 있습니다. 하지만 직선 ${l}_1$에서 벗어나지는 않습니다. 예측 불가능한 외란으로 인해 ${x}_2$나 ${x}_3$와 같이 경로에서 벗어날 수 있습니다. 하지만 PID 제어기는 그 경로에서 벗어난 현재 상태로부터 다시 직선 ${l}_2$을 만들고, 그 직선을 따라 움직이려고 합니다. 즉 목표 지점이 바뀌지 않는 한, 현재 상태가 움직이는 경로는 바뀌지 않습니다.
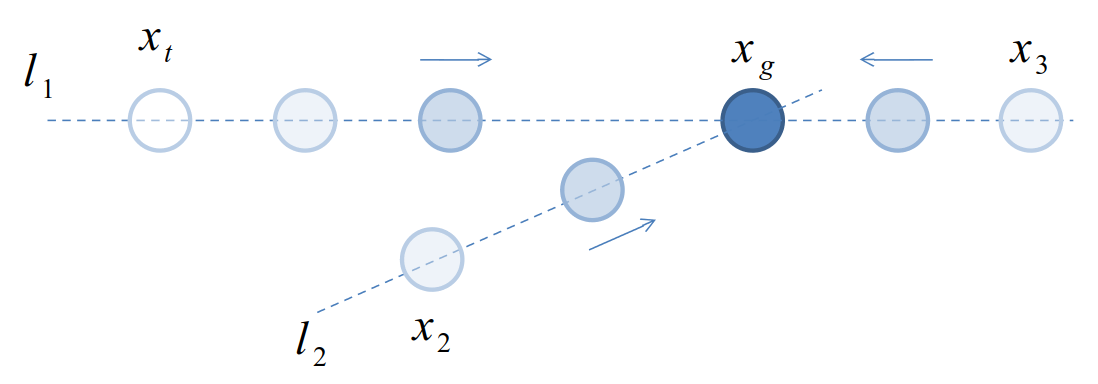
따라서 PID제어를 이용하여 복잡한 시스템을 제어하기 위해서는, 상태에 따라 목표 지점을 변경해주는 알고리즘, 즉 경로를 생성해주는 알고리즘이 추가로 필요합니다. 하나의 예로 아래와 같은 단순한 로봇팔을 생각해보겠습니다. 로봇팔이 목표 지점을 향해 움직일 때, 로봇 핸드가 직선으로 움직이려면 1번 축과 2번 축은 서로 다른 방향으로 움직여야합니다. 이 각 축의 움직이는 방향과 속도, 즉 최적 경로는 기구학이라는 추가적인 알고리즘을 이용하여 생성해야 합니다.
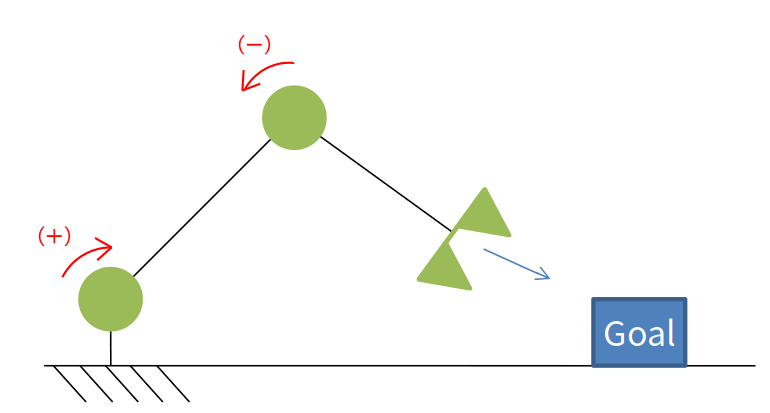
Problem in PID Control
이처럼 PID 제어를 적용하기 위해서는, 경로를 찾는 문제를 먼저 풀어야합니다. 문제는 가이드와이어의 최적 경로를 찾는 일이 매우 어렵다는 것입니다.
가이드와이어 로봇 제어의 가장 큰 문제 중 하나는, 가이드와이어가 어떠한 경로로 움직여야 목표 지점까지 도달할 수 있는지 직관적으로 알기 어렵다는 것입니다. 단순하게 생각하면 가이드와이어가 혈관의 중심선을 따라 움직이면 되는 것처럼 보입니다. 하지만 실제로는 가이드와이어와 카데터 사이의 마찰, 혈관 내벽과의 마찰 등으로 인해 중심선만 따라가서는 목표까지 도달할 수 없습니다.
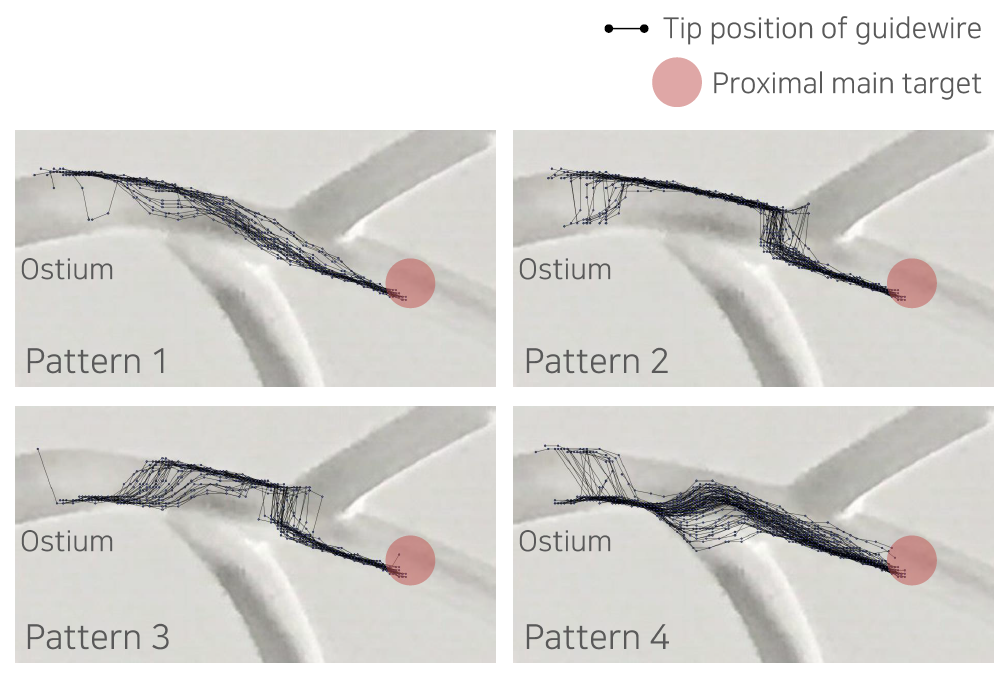
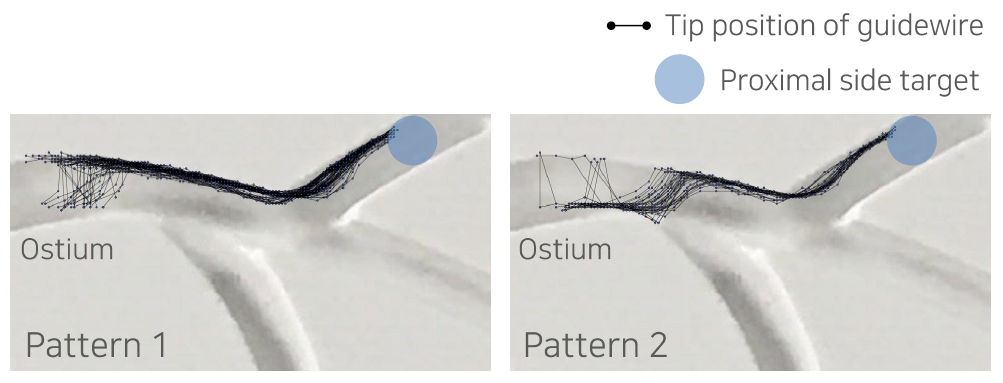
아래 그림은 저희가 수행한 실험 중 하나로, 한 개의 분지 혈관을 통과하기 위해 가이드와이어가 선택한 경로를 보여줍니다 [2]. 그림을 보시면 가이드와이어의 경로는 중심선이 아니라, 대부분 혈관 벽에서 벽으로 이동하며 상당 부분 마찰력을 이용해 움직이는 것을 알 수 있습니다. 이러한 경로는 수학적인 방법이나 직관으로 구해내기 매우 어렵습니다. 따라서 최적 경로를 쉽게 만들어낼 수 없고, 최적 경로를 얻어낼 수 없다면 PID 제어를 적용하기 어렵습니다.
Reinforcement Learning
강화학습은 이러한 문제를 푸는데 최적화되어 있습니다. 사실 강화학습과 PID 제어는 동일선 상에서 비교하는 것이 불공평할 수도 있습니다. 두 알고리즘이 각각 목표하는 바가 다르기 때문입니다. PID 제어는 위에서 말씀드렸듯이 Tracking에 최적화되어 있고, 강화학습은 최적 경로를 찾는 것에 최적화되어 있습니다.
강화학습이 목표로 하는 것은 agent가 각 상태(state)에서 보상(reward)을 최대로 하는 행동(action)을 하는 것입니다. 이러한 목표를 달성하기 위해 각 상태에서 어떤 행동을 선택하는 것이 좋은지 경험을 통해 판단합니다. 이러한 경험을 통한 판단을 정책(policy)이라고 하며, agent는 환경과 상호작용하며 얻는 보상을 최대로 하는 방향으로 정책을 업데이트 해나갑니다. 즉 강화학습 agent는 문제에 대한 최적의 정책을 찾게 되고 이는 곧 최적 경로를 찾는 것과 같습니다.
PID Control vs RL
지금까지 왜 PID 제어로는 PCI 로봇을 제어하기 어려운지 알아보았습니다. 이 두 알고리즘의 차이는 결국 최적 경로를 만들어낼 수 있는가 없는가의 차이입니다. 강화학습은 병변부위까지 가이드와이어를 이동시키는 최적의 경로를 찾는 것이 가능하지만, PID 제어로는 그 경로를 찾을 수 없습니다. 그저 경로를 따라갈 뿐입니다.
하지만 독자분들께서는 여기서 의문을 제기하실 수 있습니다. 왜냐하면 기존 제어이론에도 최적 경로를 찾는 알고리즘이 있기 때문입니다. 이는 최적제어 (Optimal Control)이라는 이론입니다. 아래부터는 이 최적제어 이론이 강화학습과 어떻게 다른지, 왜 저희는 최적경로를 위한 두 알고리즘 중에서도 강화학습을 선택하게 되었는지 이야기해보겠습니다.
Optimal Control
Optimal Control vs RL
강화학습과 최적제어는 모두 최적 경로를 찾기 위한 알고리즘입니다. 목적이 같은 만큼 두 알고리즘은 많은 면에서 유사한 모습을 보입니다. 실제로 강화학습의 아버지라고 불리는 Richard S. Sutton 교수는 최적제어의 한 부분으로서 강화학습을 활용하는 것을 제안하기도 했습니다 [3].
먼저 강화학습과 최적제어의 공통점부터 살펴보겠습니다. 강화학습과 최적제어 모두 다양한 이론들이 소개되어 있습니다. 이 글에서는 강화학습의 기초 이론 중 하나인 Dynamic Programming과, 가장 대표적인 최적제어이론 중 하나인 LQR Control (Linear Quadratic Regulator)을 비교해보도록 하겠습니다 [4][5]. 강화학습과 최적제어는 용어와 계산하는 과정만 조금 차이가 있을 뿐, 거의 동일한 개념과 구조를 갖고 있습니다. 두 방법 모두 1) 모델링, 2) 목적함수 결정, 3) 정책 결정, 4) 최적해 계산의 4개 단계를 이용하여 이 문제를 해결합니다.
예시를 위해 아래 그림과 같은 문제를 가정하겠습니다. 자동차가 목적지 Goal까지 장애물을 피하여 최대한 빨리 도달하는 것이 목표입니다.
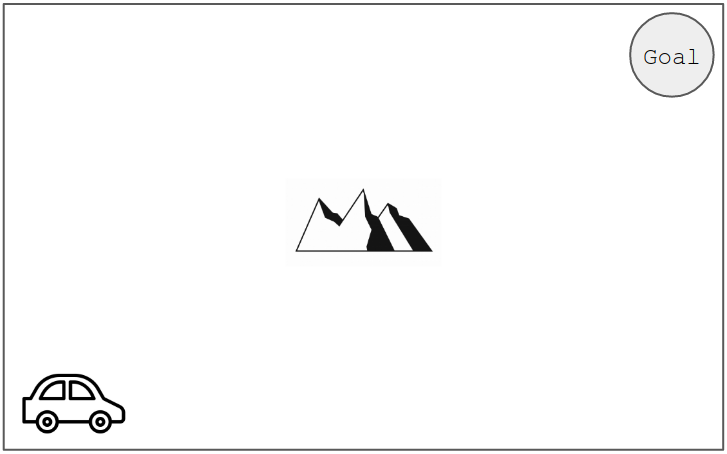
Step 1. 모델링
모델은 로봇 혹은 agent가 어떠한 동작을 취했을 때, agent의 상태나 환경이 어떻게 변하고 반응할지를 수학적으로 나타낸 것입니다. 최적경로 탐색은 정확하면서도 해를 찾을 수 있는 모델을 만드는 것에서부터 시작합니다.
Dynamic Programming : 본 글에서는 편의를 위하여 Dynamic Programming에서는 Grid 환경을 가정합니다. Grid 환경에서는 인접한 Grid 간의 이동확률인 상태전이확률 $p$로 환경이 모델링 될 수 있습니다. 현재 상태가 $s$이고, 여기서 행동 $a$를 취했을 때, 상태전이확률 $p$에 의해 다음 상태 $s’$가 결정됩니다. 이 때 발생하는 보상(reward) $r$ 또한 모델에 의해 정의됩니다. $$ p(s’,r|s,a) = Pr({S}_t=s’, {R}_t = r | {S}_{t-1}=s, {A}_{t-1}=a) $$

LQR Control : LQR 제어에서는 아래와 같은 상태 공간 방정식이라는 방법을 이용하여 환경을 모델링 합니다. 상태 공간 방정식은 주로 동역학 해석을 통해 이루어집니다. $x$는 자동차의 상태를 표현하고, $u$ 자동차의 행동, 즉 제어 입력을 의미합니다. $A$는 환경의 관성, 마찰 등 자동차와 환경의 동역학 특성을 나타냅니다. $B$는 제어 입력이 어떻게 시스템에 적용되는지 표현합니다. 산과 같은 장애물은 가까이 갔을 때 중력의 영향이 커지는 형태로 모델링하거나, 아예 산의 위치에 도달하지 못하도록 constraint 조건 $[{x}_{m,1}, {x}_{m,2}]$을 이용하여 표현할 수 있습니다.
$ \dot{x} = Ax + Bu $ subject to $ 0<x<{x}_{m,1}, \ \ {x}_{m,2}<x $ 
Step 2. 목적함수 결정
목적함수란 로봇 혹은 agent가 어떠한 경로를 선택했을 때, 그 경로를 수치적으로 평가할 수 있게 해주는 식입니다. 최적제어에서는 Performance measure라고 표현합니다. agent는 자신이 행동을 취하고 상태가 변할 때마다, 상태 전이로 인해 얻어지는 변화들을 모두 저장합니다. 이러한 정보를 이용하여 경로 하나를 마쳤을 때 그 경로에 대한 평가를 진행하게 됩니다.
Dynamic Programming : 강화학습에서는 각 상태(state)에서의 보상(reward) $R$를 이용하여 목적함수 $G$를 계산합니다. 간단하게는 단순히 지금까지 얻은 모든 보상(reward)을 더하여 얻습니다. 이러한 경우 목적함수의 출력이 무한히 커지는 문제가 있는데, 과거의 보상(reward)의 비율을 점점 줄이는 방법을 통해 (감가율(discount rate), $\gamma$) 이를 해결하기도 합니다. 강화학습은 이 목적함수를 최대화하는 것을 목표로 합니다. $${G}_t = {R}_{t+1} + \gamma {R}_{t+2} + \gamma^2 {R}_{t+3} + … = \sum_{k=0}^{\infty} \gamma^k {R}_{t+k+1}$$
LQR Control : 아래 식은 가장 일반적으로 사용되는 performance measure $J$입니다. LQR 제어는 이 $J$를 최소화하는 것을 목표로 합니다. $x$가 있는 첫번째 항은 자동차가 얼마나 빨리 목표 상태로 도달하는지 평가하는 식이고, $u$가 포함된 두번째 항은 얼마나 효율적으로 (최소한의 입력 $u$를 이용하여) 목표까지 도달하는지를 평가합니다. $Q$와 $R$은 $x$와 $u$의 중요도 비율을 바타냅니다. $$ J = \int_0^\infty (x^T Q x + u^T R u) dt $$
Step 3. 정책 결정
Dynamic Programming : 최대 state value $v(s)$를 쫓아가도록 정책 (policy) $\pi$를 설정합니다. State value란 각 상태(state)에서 미래에 얻을 수 있는 총 보상(reward)의 평균, 즉 목적함수 $G$의 기대값입니다.
${v}_\pi(s) = {\mathbb{E}}_\pi[{G}_t|{S}_t=s] $ $\pi = \underset{a}{\arg\max}\ \ v(s,a) $ LQR Control : Performance measure $J$의 $Q$와 $R$의 값을 설정하여 어떠한 요소에 가중치를 둘 지 결정합니다.
Step 4. 최적해 계산
Step 1의 모델, Step 2의 목적함수, Step 3의 정책을 이용하여, 목적함수가 최대가 되는 경로를 찾습니다. 강화학습에서는 주로 목적함수의 최대값을 찾고, 최적제어에서는 최소값을 찾습니다만, 기본 원리는 동일합니다.
Dynamic Programming : Bellman Equation과 value iteration을 이용하여 각 상태(state)에서의 value를 계산합니다. Iteration 횟수가 많아질수록 state value는 정확해지고, 이를 무한대로 수행하면 결국 하나의 값에 수렴하게 됩니다. 아래 그림은 iteration에 따라 변화하는 state value를 보여줍니다. State value가 클수록 진한 색으로 표현됩니다.
${v}_{k+1}(s) = \underset{a}{\max} \sum_{s’,r} p(s’,r|s,a) [r + \gamma{v}_k(s’)]$ 
LQR Control : 최적제어에서는 Step 1 모델의 $A$, $B$와 같은 상수 행렬을 이용하여 performance measure $J$가 최소가 되는 u를 계산합니다. u는 아래 두번째 식과 같이 상태 $x$에 대한 식으로 표현됩니다. 이 해는 Riccati Equation 등을 활용하여 구하게 되는데, 이는 본 글의 범위에서 벗어나므로 제외합니다.
minimize $ \int_0^\infty (x^T Q x + u^T R u) dt$ $$u = Kx$$
Model-free를 향해
위의 두 알고리즘의 구조를 보면, 모델의 형태와 사용하는 목적함수( or performance measure)만 다를 뿐, 그 구조는 완전히 동일하다고 해도 무방합니다. Dynamic Programming, LQR Control 두 방법 모두 모델이 있다는 것을 가정하고 문제를 풀어나갑니다. 최적제어에서는 상태 공간 방정식을 이용해 모델을 표현하고, 강화학습에서는 상태, 행동, 상태 전이 확률로 모델을 표현합니다. 이 모델을 이용하여 목적함수의 최적해를 계산하고, 그 결과에 따라 로봇에 적용되는 입력을 결정합니다.
그런데, 만약 저희가 이 모델을 구할 수 없는 상황이 되면 어떻게 될까요? 단순히 파라미터의 값이 조금 틀린 정도가 아니라, 모델에 영향을 미치는 요소가 너무 많아 모델에 다 담을 수 없다면? 실제 환경의 제약으로 인해 그 요소들을 모두 측정할 수 없는 상황에서는 어떠한 방법을 써야 할까요?
강화학습은 이 문제를 trial & error, 즉 경험을 이용한 방법으로 풀어냅니다. Dynamic Programming 이후의 강화학습 이론, Monte-Carlo, Q-learning 등이 그 예입니다. 실제 경험을 이용해 각 상태에서 목적함수의 측정값을 수집한 후에, 목적함수의 예측값과 실제 측정값이 같아지도록 목적함수를 업데이트 합니다. 목적함수를 계산하는데 환경 모델을 사용하지 않습니다. 즉, Model-free 조건에서 문제를 푸는 방법입니다 [6].
PCI 로봇 제어는 이러한 Model-free 방법이 필요합니다. 모델을 만드려면 가이드와이어에 작용하는 힘 요소들을 모두 알아야 하는데, 가이드와이어의 어느 부분이 휘어져있는지, 어느 부분이 혈관과 카데터와 닿아있는지, 가이드와이어와 혈관 사이 마찰력은 얼마나 강한지 등을 모두 알아야합니다. 이를 모두 측정할 수 있으면 좋겠지만, 아쉽게도 현재 판매 중인 가이드와이어 중 그 모든 것을 측정할 수 있는 제품은 없습니다. 심지어 이 요소들은 시간에 따라 불규칙하게 변하는, time-variant 특성을 갖고 있고, 그 변화 폭이 커 모델로 표현하기가 더더욱 어렵습니다. 결국 이러한 요소들을 경험을 통해서 알아내야 한다는 결론에 저희는 도달했습니다.
Conclusion
제어이론과 강화학습 중 저희가 왜 강화학습을 선택했는지 이야기해보았습니다. 최적경로 탐색, Model-free 접근이 가능하다는 것이 저희가 PCI 로봇에 강화학습을 적용한 가장 큰 이유입니다. 다음 글에서는 저희가 강화학습을 실제로 어떻게 PCI 로봇에 적용했는지 이야기해보겠습니다.
Reference
[1] Wikipedia (PID Controller) https://en.wikipedia.org/wiki/PID_controller
[2] J. Kweon, H. Kwon, J. Park and Y. Kim, “Reinforcement Learning for Guidewire Navigation in Coronary Phantom”, TCT 2019, San Francisco, Sep 2019.
[3] R.S. Sutton, A.G. Barto and R.J. Williams, “Reinforcement Learning is Direct Adaptive Optimal Control”, American Control Conference, Boston, June 1991.
[4] R.S. Sutton and A.G. Barto, “Reinforcement Learning: An Introduction 2nd Edition”, The MIT Press, Cambridge, 2018.
[5] D.E Kirk, “Optimal Control Theory: An Introduction”, Dover Publication, New York, 2004.
[6] C.B. Black and D.C. Rucker, “Parallel Continuum Robots: Modeling, Analysis, and Actuation-Based Force Sensing”, IEEE Transactions on Robotics, vol.34, no.1, Feb 2018.